在什么样的环境下，我们可以或许说一个系统的某本性质是稳健的（robust）？一本性质假如是稳健的，则意味着纵然系统受到了外部扰动的影响，且无论这种影响有何等强或何等随机，这种性质仍然能保持稳定。

在数学中，物体在形变方面的稳健性被称为拓扑。譬喻字母s、S、L的形状在拓扑学中就属于同一领域，具有沟通的拓扑，可以通过拉伸或弯曲它们的形状而彼此转换；字母o、O、D属于另一领域，而S和O之间不能举办这种转换，除非将O切开，或将S的两头粘在一起。也就是说，拓扑学描写的是一个物体除非被撕裂，否则无论被如何拉伸、扭曲可能畸变，城市维持稳定的特性。

在已往的几十年里，物理学家发明量子系统的某些性质只取决于系统的某些根基特征的拓扑，最著名的例子之一就是量子霍尔效应。这种现象产生在当二维的导电质料碰着垂直于它的磁场时，在这种环境下，质料中的电子会在被称为盘旋轨道的小圆圈中移动，在质料的大部门区域不会发生任何净电流，然而在质料的边沿，电子会在完成一个盘旋之前反弹，然后朝着相反的偏向移动，导致电子沿着边沿发生净活动。

这种边沿电流是独立于边沿的形状的，纵然边沿呈现强烈的形变，这种电流也能一连存在，这凸显了量子霍尔效应的稳健性。这也是为何拓扑学会被用来描写量子霍尔效应中的导电现象。

二

那么，拓扑学和生物学之间是否也存在雷同的关联呢？

生物化学网络凡是长短常巨大的，但在变革时又能维持某种不变性。这就发生了一个问题，这些生物化学系统的行为是如何做到维持得如此稳健的呢？一直以来，很多研究人员都想要将常被用于描写量子系统的拓扑模子，也用在生物学上。

在一项于近期颁发在《物理评论X》上的研究中，来自马克斯·普朗克动力学和自组织研究所的研究人员首次乐成地将拓扑的观念用在了生物化学网络上。

他们留意到，量子霍尔效应中的盘旋轨道与生物化学系统中的所谓的“无效轮回”（futile cycle）有着相似之处。在生物化学中，当两个代谢途径同时朝着相反的偏向运行，使得整个进程除了以热的形式耗损了能量之外没有发生任何整体影响时，这个轮回就被称为是“无效的”，至少乍看之下是无效的：譬喻一种化学物质A可以转换为B，B会转化为C，C又能转化回A。

研究人员模仿一个产生在二维空间中的生物化学进程。一个简朴的例子是，一种卵白质是由两种差异范例的亚基X和Y组成的。他们配置了一个顺时针的无效轮回，这个轮回所对应的进程是先添加一个Y，再添加一个X，然后移除一个Y，再移除一个X，，最终系统回到初始状态。

这样的一个二维空间也会呈现“边沿”，这个“边沿”是由亚基的可用性所导致的约束所造成的。在这个例子中，“边沿电流”对应于这个生物化学系统中的大局限轮回振荡。在研究中，他们发明这些“边沿”会自发地发生“逆时针的电流”——它们会导致一个轮回，在这个轮回中，首先所有的X亚基被添加到卵白质中，然后是所有的Y亚基添加到卵白质中，再是所有的X被移除，最后是所有的Y被移除，完成轮回。

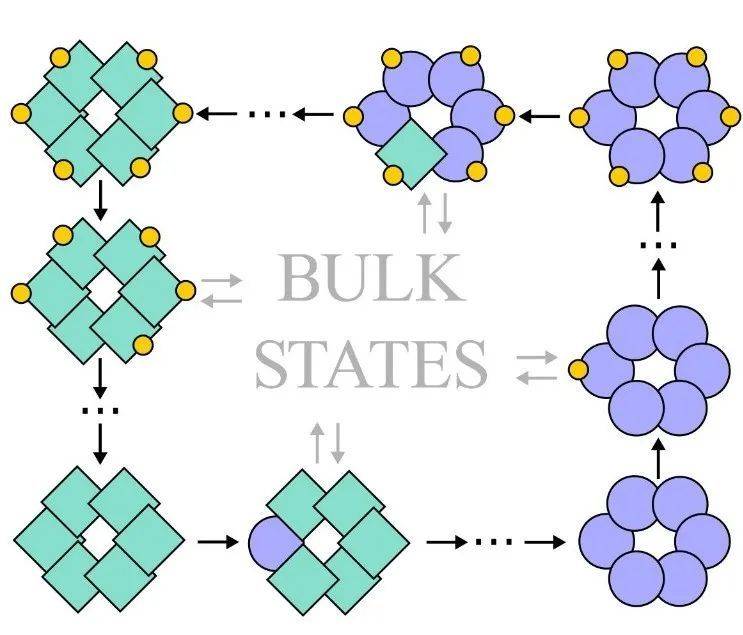
图中显示的是一个在经验边沿轮回的生物化学系统，这是一个由6个亚基（绿色方片和紫色圆形）构成的卵白质复合物，这些亚基可以改变形状或与另一个分子（黄色圆形）团结。当个中所有亚基都改变形状，然后与一个分子团结，再全部改变形状，再最后释放谁人分子，卵白质就能显示出边沿轮回。｜图片来历：Evelyn Tang et.al

这样的功效意味着，在二维的生物化学回响网络中形成了“静电流”。并且无论这种系统边沿的形状是否有变革，照旧系统整体的无序性的改变，这些生物化学“边沿电流”都显现出了稳健性。另外，研究人员还发明，边沿电流的呈现与由能源耗损驱动的无效轮回的不服衡性有着不行支解的接洽。研究人员想要知道，是否就像在量子霍尔系统中那样，生物化学系统中的这种稳健性是否也来自于拓扑。